HOW BIG IS A QUINTILLION?
When Warren Buffett put up a billion dollars for a perfect March Madness bracket, he knew his money was a lot safer than most people think. It's been calculated that the odds of someone out there picking a perfect bracket are 1 in 9,223,372,036,854,775,808. That's 9 quintillion, 223 quadrillion, 372 trillion, 36 billion, 854 million, 775 thousand, 808 possible bracket configurations. Of course it's possible, but in order to understand just how unlikey picking a perfect bracket is, we're going have to start much smaller. Let's try to win the lottery.
A million is much bigger than you think
To get a better grasp of just how enormous 9 quintillion is, it's helpful to start smaller. Let's talk about the odds of another highly unlikely event: winning the lottery. I live in the state of New York, where the lottery is a pick 6 with the numbers 1-59. Mathematicians call this a 59 choose 6 combination. It's a combination because order doesn't matter, so no matter what order the numbers come in, if they match yours you win. This eliminates A LOT of redundancies, greatly increasing your chances of winning. (When order does matter, as in license plates, it's called a permutation instead of a combination. Think: permutation, position.) Try your lucky numbers in the boxes below to simulate playing the lottery every week until you win! FYI: You may win on your first try, but if your lucky numbers aren't so lucky, you may need to leave this simulation running for days.
your lucky #s:
current winning #s:
current # of plays:
OK, I digress. So the number of possible lotto combinations is 59 choose 6 (expressed mathematically as 59C6). See the link above for the formula, or suffice it to say that it yields:
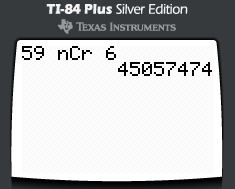
45,057,474
possible outcomes! Needless to say, a 1 in 45 million chance is pretty unlikely. But compared to your odds of picking a perfect bracket, it's like comparing a free throw to a full court buzzer-beater.
Back to that quintillion
The 9.2 quintillion number comes from the fact that there are 63 games in the tournament, each with 2 possible outcomes (either one team wins or the other one does). According to the Fundamental Counting Principle, this yields
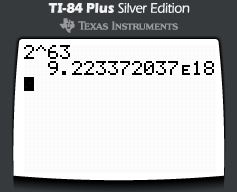
This number is so large that the calculator cannot display it all on one line, so it is expressing it in Scientific Notation. However, Wolfram Alpha can do it!
263 = 9,223,372,036,854,775,808
possible combinations! This number is so massive that human beings have a hard time imagining it. We simply have no frame of reference for numbers that large. The great astrophysicist Neil deGrasse Tyson pointed out that, counting at the impressive rate of one number per second, it would take you 12 days to reach a million, but 32 years to reach a billion, and "32,000 years to reach a trillion, which is as much time as has elapsed since people first drew on cave walls!" At that rate, since a quadrillion is a thousand trillions, and a quintillion is a thousand quadrillions, it would take you 32 billion years to reach a quintillion, which is more than twice the age of the universe!
Here's another good frame of reference, again from Tyson. "Last I checked, Bill Gates was worth $50 billion. If the average employed adult, who is walking in a hurry, will pick up a quarter from the sidewalk, but not a dime, then the corresponding amount of money (given their relative wealth) that Bill Gates would ignore if he saw it lying on the street is $25,000."
Lastly, check out how big a trillion dollars is (IN THE FORM OF PALLETS OF HUNDRED DOLLAR BILLS) at: pagetutor.com!
So 9 quintillion is a big number for sure, but how much bigger than that 1 in 45 milllion chance of winning the lotto?
Improving your odds
Of course, this assumes you know nothing about college hoops and just flip a coin to predict the winner of each game — ignoring facts such as no 16 seed has ever beaten a 1 seed, so those games are far more certain than 50-50.
Laura McLay, an associate professor of engineering at the University of Wisconsin at Madison, says that even if you do your research, your odds of picking the perfect bracket are still roughly
1 in 128,000,000,000
(1 in 128 billion)! This means that you are
128 B⁄45 M ≈ 2,844 times
more likely to win the lottery than to pick a perfect bracket! Assuming the 1 in 128 billion odds, USA Today pointed out that if we estimate that 25 million brackets are filled out online every year, we'd see a perfect one roughly every 5,000 years! When you look at it that way, it's no surprise that the last man standing this year only got just past halfway to perfection. And keep in mind, you're far more likely to
- live to 100 (1 in 5,780)
- be murdered (1 in 18,989)
- be struck by lightning (1 in 700,000)
- die in a plane crash (1 in 11,000,000) or even
- have identical quadruplets (1 in 13,000,000)
To sum it up
So you're more than 3 times more likely to have have identical quadruplets than to win the lotto. Take a moment to count all all the sets of identical quadruplets you know. Zero? Same. These are extremely rare events. But you are 2,844 times more likely to pick the winning numbers than to pick the winning bracket! But I'm still gonna play because, like they say,

